Options Greeks

Delta
Delta measures how much the options value may change with a $1 move in the underlying price. Deltas are impacted by changes in stock price, Tooltip , and time to expiration.
Delta provides a theoretical measure of the options probability of expiring in-the-money. For example, an options contract with a delta of 0.33 has a theoretical 33% chance of closing in-the-money.
Calls have positive deltas (0 to +1.00) and a positive correlation to stock price changes. Puts have negative deltas (0 to -1.00) and a negative correlation to stock price changes.
Keep in mind, as expiration approaches:
• In-the-money options have deltas approaching 1.00
• At-the-money options have deltas closer to .50
• Out-of-the-money options have deltas approaching 0
Learn more about options delta, options probability, and other risk factors.
Theta
Theta is the expected decrease in an options price as time passes, known as time decay. Typically, as expiration approaches, options lose value at a faster pace due to time decay, especially for at-the-money options. Generally, time decay works against options buyers and favors options sellers.
Theta is highest for at-the-money options and lowest for in-the-money or out-of-the-money options.
Changes in implied volatility will impact changes in theta.
Learn more about strategies for using theta.
Gamma
Gamma measures and gauges how much delta is expected to change with each $1 move in the underlying price.
Gamma conveys how sensitive the options price is to the underlying price changes. Gamma will be larger for at-the-money options and smaller for both in-the-money and out-of-the-money options. Gamma also increases and becomes more sensitive as options contracts approach expiration.
Learn more about how to use gamma.
Vega
Vega is a measure of how a change in implied volatility may affect an options price. Long options have positive vega, and short options have negative vega.
Vega measures the theoretical price change of an options contract based on a 1% movement in implied volatility. Since implied volatility is based on the market's assessment of volatility until expiration, vega increases as the market thinks there will be more variability in the underlying price. Vega is also impacted by time to expiration; longer-dated expirations have a higher vega than those close to expiration.
Vega is highest for at-the-money strikes because that's where the highest time value exists.
Learn more about Greeks with our educational course.
Schwab clients can log in for an in-depth course that introduces the concepts of Greeks, including strategies for using them in thinkorswim®.
Explore the basics of Greeks in our Options for Beginners: Income Strategies course.
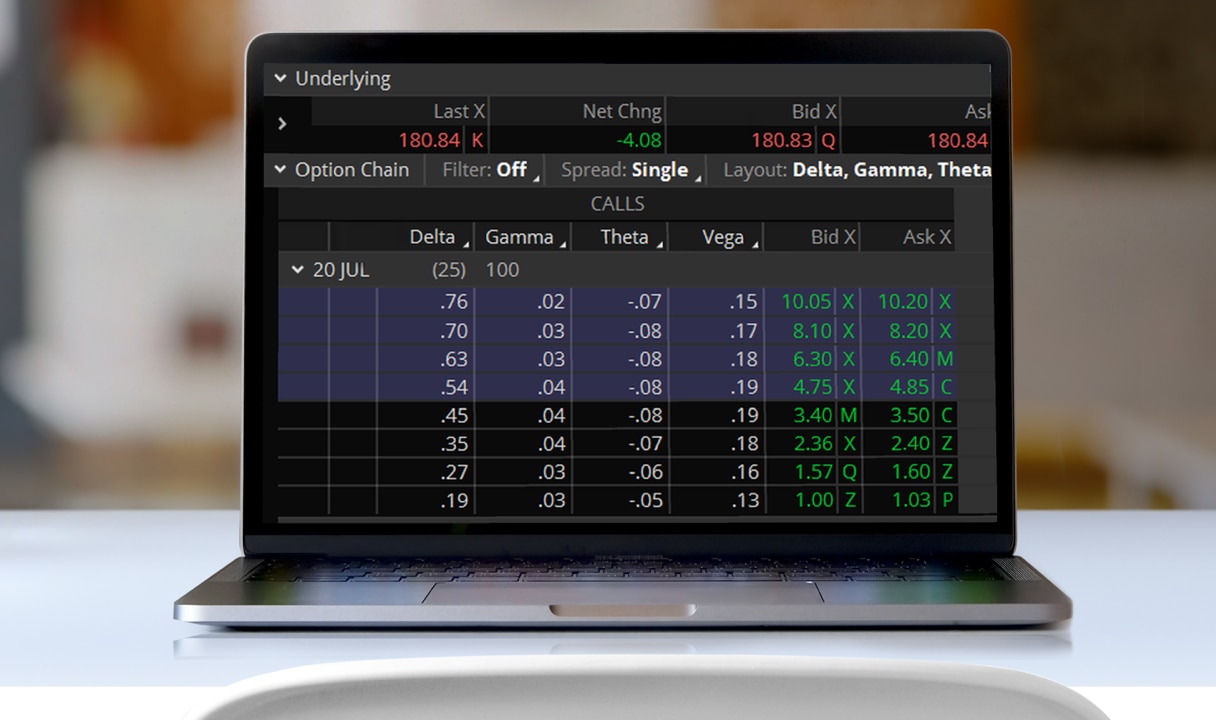
Using options Greeks in thinkorswim
You don't need to be an expert on the math used to calculate options price changes. Schwab's thinkorswim trading platform allows you to easily configure an options chain to show the Greeks for each strike.
Learn more about thinkorswim.